Differentiation - Implicit Differentiation and Inverse Functions(1)

지난 글들을 통해 도함수를 찾기 위한 몇 가지 공식들에 대해 알아보았습니다.  이번 글부터는 연쇄 법칙(Chain Rule)을 이용하여 좀 더 다양한 함수들의 도함수를 구하는 것을 목표로 합니다. 이번 글에서는 음함수의 미분법에 대해 써보려고 합니다.

---

Implicit Differentiation (Rational Exponent Rule)

---

n이 정수일 때, y = x^n의 도함수는 dy/dx = nx^(n - 1)임을 알고 있습니다. 그렇다면, n이 정수가 아닐 때에도 이 공식은 참일까요?

$$\frac{d}{dx}(x^a)=a{x}^{(}a-1)$$

지난 글에서 이항 정리와 도함수의 정의를 이용하여 정수 a에 대해 위 사실을 증명했습니다. 이제 이 공식을 정수를 넘어 유리수까지 확장하여 a = m/n일 때에도 살펴보겠습니다.

$$y=x^{\frac{m}{n}}$$

m과 n이 정수인 상황에서 위와 같은 공식이 주어졌을 때, dy/dx를 구하고자 합니다. 슬프게도 이와 관련해서 이전 글에선 알아본 것이 없습니다. 도함수의 정의를 이용하려 해도 지수의 형태가 유리수인 점이 발목을 잡네요. 이걸 해결하기 위해 양변을 n제곱하겠습니다.

$$\begin{array}{rl}y& =x^{\frac{m}{n}}\\ y^n& =(x^{\frac{m}{n}}{)}^n\\ y^n& =x^{\frac{m}{n}\cdot n}\\ y^n& =x^m\end{array}$$

이제 d/dx를 양변에 적용하려 하는데, d/dx(y^n)을 어떻게 계산해야 할까요? 우리는 y가 x에 대한 함수임을 알 수 있습니다. 따라서, u=y^n으로 치환을 한 후, 연쇄 법칙을 적용하면 다음과 같이 해결할 수 있습니다.

$$\begin{array}{rl}\frac{du}{dx}& =\frac{du}{dy}\frac{dy}{dx}\\ \therefore \frac{d}{dx}{y}^n& =(\frac{d}{dy}{y}^n)\frac{dy}{dx}=n{y}^{n-1}\frac{dy}{dx}\end{array}$$

그리고 우변은 다음과 같이 정리가 가능합니다.

$$\begin{array}{rl}\frac{d}{dx}{y}^n& =\frac{d}{dx}{x}^m\\ \therefore n{y}^{n-1}\frac{dy}{dx}& =m{x}^{m-1}\end{array}$$

이제 dy/dx만 해결하면 됩니다. 양변을 ny^(n-1)로 나누어주면, 다음을 얻을 수 있습니다.

$$\frac{dy}{dx}=\frac{m}{n}\$\frac{x^{m-1}}{y^{n-1}}$$

이것도 괜찮지만, 저희는 y는 빼고 x만 보고 싶죠. y를 없애기 위해 y=m^(m/n)을 대입하겠습니다.

$$\begin{array}{rl}\frac{dy}{dx}& =\frac{m}{n}(\frac{x^{m-1}}{y^{n-1}})\\ & =\frac{m}{n}(\frac{x^{m-1}}{(x^{m/n}{)}^{(n-1)}})\\ & =\frac{m}{n}(\frac{x^{m-1}}{x^{(m/n)\cdot (n-1)}})\\ & =\frac{m}{n}\frac{x^{m-1}}{x^{m(n-1)/n}}\\ & =\frac{m}{n}{x}^{((m-1)-\frac{m(n-1)}{n})}\\ & =\frac{m}{n}{x}^{\frac{n(m-1)}{n}-\frac{m(n-1)}{n}}\\ & =\frac{m}{n}{x}^{\frac{n(m-1)-m(n-1)}{n}}\\ & =\frac{m}{n}{x}^{\frac{nm-n-nm+m}{n}}\\ & =\frac{m}{n}{x}^{\frac{m-n}{n}}\\ & =\frac{m}{n}{x}^{(\frac{m}{n}-\frac{n}{n})}\\ \therefore \frac{dy}{dx}& =\frac{m}{n}{x}^{(\frac{m}{n}-1)}\end{array}$$

이제 원하던 답을 얻었습니다. a가 유리수일 때에도 x^a의 도함수가 ax^(a-1)이라는 사실을 알게 되었습니다.

---

Derivative of the Inverse of a Function

---

음미분의 응용 중에서 가장 중요한 것은 역함수의 도함수를 찾는 것입니다. 간단한 예제에서 시작하겠습니다. 0 보다 큰 x에 대해 y = sqrt(x)라는 식에서 양변을 제곱하여 y^2 = x를 얻습니다. y = f(x) = sqrt(x)라 하고, 이에 대한 역함수 f^(-1) = g(x) = x ^ 2를 설정하겠습니다.

Figure 1: The graph of g is the reflection of the graph of f across the line y = x

일반적으로, 함수 f의 그래프를 갖고 있다면 이를 y축과 x축을 교환하는 것으로 함수 f의 역함수의 그래프 역시 그려낼 수 있습니다. 다르게 말해서, 함수 f의 역함수의 그래프는 y = x를 기준으로 함수 f의 그래프를 반전시킨 것이라고도 할 수 있습니다. 이는 dy/dx가 함수 f에 대한 접선의 기울기라면 dx/dy가 함수 f의 역함수의 기울기가 될 것이라는 말입니다. 이 사실을 증명하기 위해 도함수의 정의를 이용할 수도 있지만, 음함수의 미분법을 사용하는 것이 더 쉽습니다.

$$\begin{array}{rl}y& =f(x)\\ f^{-1}(y)& =x\\ \frac{d}{dx}(f^{-1}(y))& =\frac{d}{dx}(x)=1\end{array}$$

연쇄 법칙에 의해 다음과 같이 됩니다.

$$\begin{array}{rl}\frac{d}{dy}(f^{-1}(y))\frac{dy}{dx}& =1\\ \therefore \frac{d}{dy}(f^{-1}(y))& =\frac{1}{\frac{dy}{dx}}\end{array}$$

이렇게 음함수의 미분법을 통해 원래 함수인 함수 f의 도함수를 알고 있다면, 이 함수의 역함수의 도함수 역시 알아낼 수 있다는 사실을 알게 되었습니다.

---

Derivative of arctan(x)

---

이제 역함수의 미분법을 알게 되었으니, 이를 이용해서 탄젠트 함수의 역함수인 아크탄젠트 함수의 도함수를 구해보겠습니다. 우선, 양변에 탄젠트 함수를 취하여 다음과 같이 정리하도록 하겠습니다.

$$\begin{array}{rl}y& ={\text{tan}}^{-1}x\\ \text{tan }y& =\text{tan}({\text{tan}}^{-1}x)\\ \text{tan }y& =x\end{array}$$

어떻게 그려지게 될지 예측해 보기 위해 탄젠트 함수의 그래프를 그려보겠습니다.

Figure 2: Graph of the tangent function.

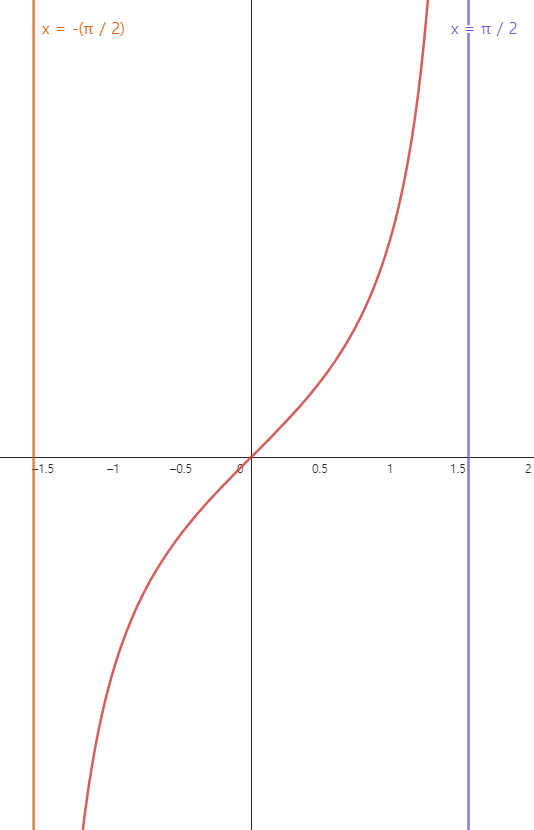
-π/2 < x < π/2에서 정의되어 있고, 음의 무한대에서 양의 무한대까지 뻗어나가는군요. 이 탄젠트 함수의 그래프를 y = x의 그래프를 기준으로 반전한다면 아크탄젠트 함수의 그래프를 얻을 수 있을 것입니다. 그렇게 되면 x의 범위와 y의 범위 역시 바뀌겠죠.

Figure 3: Graph of the inverse of the tangent function.

$$\begin{array}{rl}\frac{d}{dy}\text{tan }y& =\frac{d}{dy}\frac{\text{sin }y}{\text{cos }y}\\ & ⋮\\ & =\frac{1}{{\text{cos}}^{2}y}\\ & ={\text{sec}}^{2}y\end{array}$$

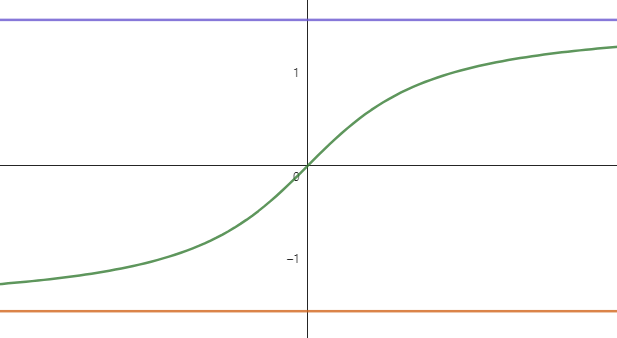
몫의 미분을 통해 위와 같은 사실은 이미 알고 있습니다. 이제 양변의 도함수를 구하기 위해 음함수의 미분법을 사용하겠습니다.

$$\begin{array}{rl}\text{tan }y& =x\\ \frac{d}{dx}(\text{tan}(y))& =\frac{d}{dx}x\\ \frac{d}{dx}(\text{tan}(y))& =1\\ (\frac{1}{{\text{cos}}^2(y)})\frac{dy}{dx}& =1\\ \frac{dy}{dx}& ={\text{cos}}^2(y)\end{array}$$

아쉽게도 우리는 x에 대한 도함수를 얻길 원하는 것이지, y에 대한 도함수를 얻고자 하는 것이 아닙니다. 따라서, 원래 공식인 y=arctan(x)를 대입해서 y'=cos^2(arctan(x))를 얻습니다. 이대로 끝내도 괜찮지만, 더 간소화할 수 있습니다.

tan(y) = x일 때, y=arctan(x)입니다. 피타고라스의 정리에 따라 빗변의 길이 h에 대해 다음이 성립합니다.

$$h=\sqrt{1+x^2}$$

그리고 이제 다음과 같이 계산할 수 있습니다.

$$\text{cos}(y)=\frac{1}{\sqrt{1+x^2}}$$

이것으로부터 다음과 같이 정리할 수 있습니다.

$$\begin{array}{rl}{\text{cos}}^2(y)=(\frac{1}{\sqrt{1+x^2}}{)}^2& =\frac{1}{1+x^2}\\ \therefore \frac{dy}{dx}& =\frac{1}{1+x^2}\end{array}$$

따라서, 다음과 같이 마칠 수 있습니다.

$$\frac{d}{dx}\text{arctan}(x)=\frac{1}{1+x^2}$$

---

Derivative of arcsin(x)

---

마지막 예시로, 아크사인의 도함수를 구해보겠습니다. 아크코사인의 경우에는 아크사인을 활용하면 쉽게 구할 수 있으니, 아크사인만 구하겠습니다. y=arcsin(x)인  식을 sin(y)=x로 고치겠습니다. 그 뒤에, 양 변의 도함수를 구해봅시다.

$$\begin{array}{rl}\text{sin }y& =x\\ (\text{cos }y)\cdot y^{\prime }& =1\\ y^{\prime }& =\frac{1}{\text{cos }y}\end{array}$$

여기서, cos^2 x + sin^2  x = 1이라는 식을 이용하여 다음의 결과를 만들어냅시다.

$$\begin{array}{rl}{\text{cos}}^{2}y+{\text{sin}}^{2}y& =1\\ {\text{cos}}^{2}y& =1-{\text{sin}}^{2}y\\ \text{cos }y& =\sqrt{1-{\text{sin}}^{2}y}\end{array}$$

이제 이 둘을 조합하여 다음의 결과로 이끌어냅시다.

$$y^{\prime }=\frac{1}{\text{cos }y}=\frac{1}{\sqrt{1-{\text{sin}}^{2}y}}=\frac{1}{\sqrt{1-x^2}}$$

이렇게 아크사인의 도함수를 구했습니다.

다음 글에서 뵙겠습니다.