Differentiation - Definition and Basic Rules(3)

모든 것을 미분할 수 있게 되기 위해 이번 글에서는 몇 가지 유용한 공식을 더 소개하고자 합니다. 도함수 공식은 2가지 유형으로 나눌 수 있습니다. 하나는 Power Rule이나, 1/x의 도함수와 같은 특정한 경우입니다. 이전 글들을 통해 다뤘었죠. 다음은 일반적인 경우에 적용할 수 있는 공식입니다. 특정 함수에 대한 공식이 아니라 (u + v)' = u' + v'나 (cu)' = cu'(c는 상수)와 같은 보편적인 경우입니다.

다항식의 도함수를 얻기 위해서는 두 공식 모두 필요하겠죠. 이번에는 몇 가지 공식을 더 소개한 뒤에 sin 함수와 cos 함수를 미분하는 것에 초점을 맞춰보겠습니다.

---

Derivative of a Sum

---

$$(u + v)'(x) = u'(x) + v'(x)$$

이번에는 위의 공식에 대해 설명해보겠습니다((u + v)(x)는 u(x) + v(x)를 의미합니다).

다르게 말해서, 두 함수의 합의 도함수는 그 두 함수의 도함수를 더한 것과 같습니다. 함수의 종류에 상관 없이 도함수를 구할 수 있는 함수라면 해당되는 사실입니다. u와  v가 어떤 함수인지 모르기 때문에 오로지 도함수의 정의만을 사용해야합니다. 도함수의 정의를 (u + v)(x)에 적용하면 다음과 같습니다.

$$(u + v)'(x) = \displaystyle \lim_{\Delta x \to 0}\frac{(u + v)(x + \Delta x) - (u + v)(x)}{\Delta x}$$

(u + v)(x)는 u(x) + v(x)와 같기 때문에 다음과 같이 바꿀 수 있습니다.

$$(u + v)'(x) = \displaystyle \lim_{\Delta x \to 0}\frac{u(x + \Delta x) + v(x + \Delta x) - u(x) - v(x)}{\Delta x}$$

그리고 다음과 같이 순서를 조금 바꿔보겠습니다.

$$(u + v)'(x) = \displaystyle \lim_{\Delta x \to 0}\left \{\frac{u(x + \Delta x) - u(x)}{\Delta x} + \frac{v(x + \Delta x) - v(x)}{\Delta x}  \right \}$$

함수 u와 v는 미분 가능하(고 연속적이)기 때문에, 위 식은 다음과 같이 바꿀 수 있습니다.

$$(u + v)'(x) = \displaystyle \lim_{\Delta x \to 0}\frac{u(x + \Delta x) - u(x)}{\Delta x} + \displaystyle \lim_{\Delta x \to 0}\frac{v(x + \Delta x) - v(x)}{\Delta x}$$

그리고 이 형태는 각각 u와 v라는 함수에 대한 도함수의 정의에 부합합니다. 이 과정을 통해 (u + v)'(x) = u'(x) + v'(x)라는 사실을 알게 되었습니다.

---

Derivative of sin x, Algebraic Proof

---

이번에는 sin x의 도함수를 구해보도록 하겠습니다. 도함수의 정의에 맞춰 생각을 해보면, 다음과 같이 적을 수 있습니다.

$$\frac{d}{dx}\textrm{sin }x = \displaystyle \lim_{\Delta x \to 0}\frac{\textrm{sin}(x + \Delta x) - \textrm{sin}(x)}{\Delta x}$$

그리고, sin함수의 각도 합 공식을 적용하면 이렇게 바꿀 수 있습니다.

$$\frac{d}{dx}\textrm{sin }x=\displaystyle \lim_{\Delta x \to 0}\frac{\textrm{sin }x\textrm{ cos }\Delta x+\textrm{cos }x\textrm{ sin }\Delta x-\textrm{sin }(x)}{\Delta x}$$

그리고 이 수식은 다음과 같이 정리할 수 있습니다.

$$\begin{align*}
\frac{d}{dx}\textrm{ sin }x &= \displaystyle \lim_{\Delta x \to 0}[\frac{\textrm{sin }x \textrm{ cos }\Delta x-\textrm{sin }x}{\Delta x}+\frac{\textrm{cos }x\textrm{ sin }\Delta x}{\Delta x}]\\ 
 &= \displaystyle \lim_{\Delta x \to 0}[\frac{\textrm{sin }x (\textrm{cos }\Delta x-1)}{\Delta x}+\frac{\textrm{cos }x\textrm{ sin }\Delta x}{\Delta x}]\\ 
 &= \displaystyle \lim_{\Delta x \to 0}[\textrm{sin }x(\frac{\textrm{cos }\Delta x - 1}{\Delta x})+\textrm{cos }x(\frac{\textrm{sin }\Delta x}{\Delta x})]\\ 
 &= \displaystyle \lim_{\Delta x \to 0}\textrm{sin }x(\frac{\textrm{cos }\Delta x-1}{\Delta x})+\displaystyle \lim_{\Delta x \to 0}\textrm{cos }x(\frac{\textrm{ sin }\Delta x}{\Delta x})
\end{align*}$$

이제 좀 익숙한 형태로 정리되었네요. 그런데, 사실 저 두 형태는 이전 글에서 제거 가능한 불연속성(Removable Discontinuitiy)에 대해 설명할 때 본 적이 있습니다. 아직 증명하지는 못했지만, x가 0의 극한값을 가질 때 sin 함수의 도함수와 cos 함수의 도함수가 각각 1과 0이라는 극한값을 가진다는 사실을 사용하도록 하죠.

$$\frac{d}{dx}\textrm{ sin }x = \textrm{sin }x \cdot 0 + \textrm{cos }x \cdot 1 = \textrm{cos }x$$

그러면 이렇게 sin 함수의 도함수가 cos 함수라는 사실을 알아낼 수 있습니다.

---

Derivative of cos x

---

이번에는 cos 함수의 도함수를 구해보겠습니다. cos 함수의 도함수를 구하는 과정은 sin 함수의 도함수를 구하는 과정과 매우 유사합니다. 그렇기 때문에 중간에 막히시면 위의 sin 함수의 도함수를 구하는 과정을 참고하시면서 읽으시면 될 것 같습니다.

$$\frac{d}{dx}\textrm{ cos }x=\displaystyle \lim_{\Delta x \to 0}\frac{\textrm{cos}(x + \Delta x)-\textrm{cos}(x)}{\Delta x}$$

sin 함수의 도함수를 구할 때 처럼 시작은 도함수의 정의로 합니다. 그리고 여기서 cos 함수의 각도 합 공식을 적용합니다.

$$\begin{align*}
\frac{d}{dx}\textrm{ cos }x &= \displaystyle \lim_{\Delta x \to 0}\frac{\textrm{cos }x\textrm{ cos }\Delta x-\textrm{sin }x \textrm{ sin }\Delta x-\textrm{cos }x}{\Delta x}\\ 
 &= \displaystyle \lim_{\Delta x \to 0}[\frac{\textrm{cos }x\textrm{ cos }\Delta x-\textrm{cos }x}{\Delta x}+\frac{-\textrm{sin }x\textrm{ sin }\Delta x}{\Delta x}]\\ 
 &= \displaystyle \lim_{\Delta x \to 0}[\frac{\textrm{cos }x(\textrm{cos }\Delta x-1)}{\Delta x}+\frac{-\textrm{sin }x\textrm{ sin }\Delta x}{\Delta x}]\\ 
 &= \displaystyle \lim_{\Delta x \to 0}[\textrm{cos }x(\frac{\textrm{cos }\Delta x-1}{\Delta x})+(-\textrm{sin }x)(\frac{\textrm{sin }\Delta x}{\Delta x})]\\ 
 &= \displaystyle \lim_{\Delta x \to 0}\textrm{cos }x(\frac{\textrm{cos }\Delta x-1}{\Delta x})+\displaystyle \lim_{\Delta x \to 0}(-\textrm{sin }x)(\frac{\textrm{sin }\Delta x}{\Delta x})
\end{align*}$$

그리고 sin x의 도함수를 구할 때 사용했던 (아직 증명하지 못한) 사실을 사용하겠습니다.

$$\begin{align*}
\frac{d}{dx}\textrm{ cos }x &= \displaystyle \lim_{\Delta x \to 0}\textrm{cos }x(\frac{\textrm{cos }\Delta x-1}{\Delta x})+\displaystyle \lim_{\Delta x \to 0}(-\textrm{sin }x)(\frac{\textrm{sin }\Delta x}{\Delta x})\\ 
 &= \textrm{cos }x\cdot 0 + (-\textrm{sin }x) \cdot 1\\ 
 &= -\textrm{sin }x
\end{align*}$$

그러면 위와 같이 정리되고, cos 함수의 도함수는 -sin 함수라는 사실을 알아낼 수 있습니다.

---

Limit of sin(x)/x

---

sin 함수와 cos 함수의 도함수를 구하는 과정에서 x가 0의 극한값을 가질 때 sin(x)/x=1이라는 극한값을 사용해야했습니다. 당시에는 증명을 하지 않고 사용했지만, 이제는 증명을 해야할 때죠.

Figure 1: A circle of radius 1 with an arc of angle θ

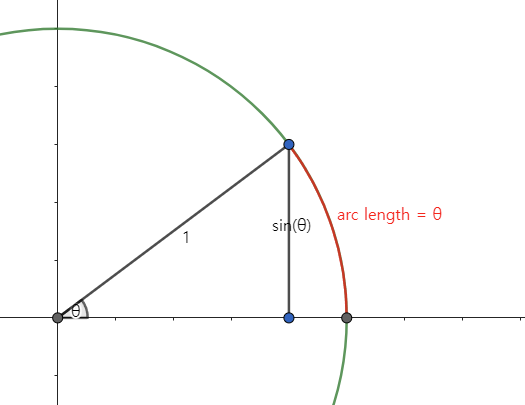
이 극한값을 구하기 위해 sin 함수의 값을 Figure 1에 표시된 것처럼 θ에 따른 단위원 위의 점의 y좌표로 간주합니다. 반지름이 1인 원에서 sin 함수의 값은 빗변으로 각의 맞은편(높이)를 나눈 값과 같습니다 . 따라서, sin(θ)/θ라 함은 높이와 호의 비율이라고도 할 수 있는데, θ가 π/2 rad 일 때 sin(θ)는 1이고, sin(θ)/θ = 2/π ≅ 2/3입니다. θ가 π/4 rad 라면 sin(θ)의 값은 (루트 2)/2 가 될 것이고, sin(θ)/θ의 값은 2(루트 2)/π ≅ 9/10이 될 것입니다. 그렇다면, θ가 이렇게 점점 줄어들어 0 rad에 가까워지면 어떻게 될까요?

$$\displaystyle \lim_{\theta \to 0}\frac{\textrm{sin }\theta}{\theta}=1$$

θ의 값은 계속해서 줄어들고, sin(θ)의 값 역시 점점 줄어들어 호의 길이와 매우 가까워지게 될 것입니다. 그리고 호의 길이는 θ의 값과 같죠. 결국 1에 매우 가까워지게 될 것입니다.

---

Limit of (1-cos(x))/x

---

x가 0의 극한값을 가질 때 (1-cos(x))/x=0이라는 극한값을 사용해야했습니다. 당시에는 증명을 하지 않고 사용했지만, 이제 증명을 해야할 때가 왔습니다. 위의 방식 처럼, 이번에도 단위원을 활용해서 설명을 하도록 하겠습니다.

Figure 2

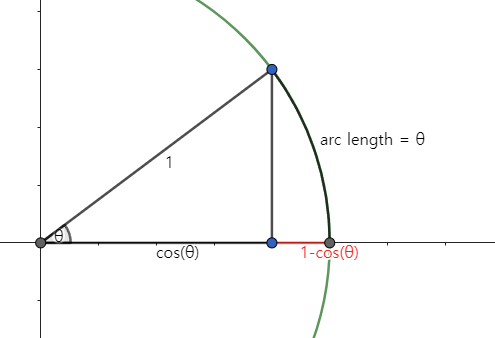
Figure 2에서 θ가 0으로 갈 때, 1-cos(θ)의 길이가 호의 길이(θ)보다 훨씬 작아지는 것을 확인할 수 있습니다. 따라서, 0/0 꼴로 보이지만 전혀 아니라는 것을 알 수 있고, θ가 작을 때 1-cos(θ)가 훨씬 더 작다는 것을 알 수 있습니다. 이런 사실을 기반으로 x가 0의 극한값을 갖도록 하면 (1-cos(x))/x는 0을 극한값으로 갖게 되는 것입니다.

다음 글에서 뵙겠습니다.