CODICT
Differentiation - Implicit Differentiation and Inverse Functions(1) 본문
Differentiation - Implicit Differentiation and Inverse Functions(1)
Foxism 2023. 4. 25. 15:34지난 글들을 통해 도함수를 찾기 위한 몇 가지 공식들에 대해 알아보았습니다. 이번 글부터는 연쇄 법칙(Chain Rule)을 이용하여 좀 더 다양한 함수들의 도함수를 구하는 것을 목표로 합니다. 이번 글에서는 음함수의 미분법에 대해 써보려고 합니다.
Implicit Differentiation (Rational Exponent Rule)
n이 정수일 때, y = x^n의 도함수는 dy/dx = nx^(n - 1)임을 알고 있습니다. 그렇다면, n이 정수가 아닐 때에도 이 공식은 참일까요?
$$\frac{d}{dx}(x^a)=ax^(a-1)$$
지난 글에서 이항 정리와 도함수의 정의를 이용하여 정수 a에 대해 위 사실을 증명했습니다. 이제 이 공식을 정수를 넘어 유리수까지 확장하여 a = m/n일 때에도 살펴보겠습니다.
$$y=x^{\frac{m}{n}}$$
m과 n이 정수인 상황에서 위와 같은 공식이 주어졌을 때, dy/dx를 구하고자 합니다. 슬프게도 이와 관련해서 이전 글에선 알아본 것이 없습니다. 도함수의 정의를 이용하려 해도 지수의 형태가 유리수인 점이 발목을 잡네요. 이걸 해결하기 위해 양변을 n제곱하겠습니다.
$$\begin{align*}
y &= x^{\frac{m}{n}}\\
y^n &= (x^{\frac{m}{n}})^n\\
y^n &= x^{\frac{m}{n}\cdot n}\\
y^n &= x^m
\end{align*}$$
이제 d/dx를 양변에 적용하려 하는데, d/dx(y^n)을 어떻게 계산해야 할까요? 우리는 y가 x에 대한 함수임을 알 수 있습니다. 따라서, u=y^n으로 치환을 한 후, 연쇄 법칙을 적용하면 다음과 같이 해결할 수 있습니다.
$$\begin{align*}
\frac{du}{dx} &= \frac{du}{dy}\frac{dy}{dx}\\
\therefore \frac{d}{dx}y^n &= (\frac{d}{dy}y^n)\frac{dy}{dx}=ny^{n-1}\frac{dy}{dx}
\end{align*}$$
그리고 우변은 다음과 같이 정리가 가능합니다.
$$\begin{align*}
\frac{d}{dx}y^n &= \frac{d}{dx}x^m\\
\therefore ny^{n-1}\frac{dy}{dx} &= mx^{m-1}
\end{align*}$$
이제 dy/dx만 해결하면 됩니다. 양변을 ny^(n-1)로 나누어주면, 다음을 얻을 수 있습니다.
$$\frac{dy}{dx}=\frac{m}{n}$\frac{x^{m-1}}{y^{n-1}}$$
이것도 괜찮지만, 저희는 y는 빼고 x만 보고 싶죠. y를 없애기 위해 y=m^(m/n)을 대입하겠습니다.
$$\begin{align*}
\frac{dy}{dx} &= \frac{m}{n}(\frac{x^{m-1}}{y^{n-1}})\\
&= \frac{m}{n}(\frac{x^{m-1}}{(x^{m/n})^{(n-1)}})\\
&= \frac{m}{n}(\frac{x^{m-1}}{x^{(m/n) \cdot (n-1)}})\\
&= \frac{m}{n}\frac{x^{m-1}}{x^{m(n-1)/n}}\\
&= \frac{m}{n}x^{((m-1)-\frac{m(n-1)}{n})}\\
&= \frac{m}{n}x^{\frac{n(m-1)}{n}-\frac{m(n-1)}{n}}\\
&= \frac{m}{n}x^{\frac{n(m-1)-m(n-1)}{n}}\\
&= \frac{m}{n}x^{\frac{nm-n-nm+m}{n}}\\
&= \frac{m}{n}x^{\frac{m-n}{n}}\\
&= \frac{m}{n}x^{(\frac{m}{n}-\frac{n}{n})}\\
\therefore \frac{dy}{dx} &= \frac{m}{n}x^{(\frac{m}{n}-1)}
\end{align*}$$
이제 원하던 답을 얻었습니다. a가 유리수일 때에도 x^a의 도함수가 ax^(a-1)이라는 사실을 알게 되었습니다.
Derivative of the Inverse of a Function
음미분의 응용 중에서 가장 중요한 것은 역함수의 도함수를 찾는 것입니다. 간단한 예제에서 시작하겠습니다. 0 보다 큰 x에 대해 y = sqrt(x)라는 식에서 양변을 제곱하여 y^2 = x를 얻습니다. y = f(x) = sqrt(x)라 하고, 이에 대한 역함수 f^(-1) = g(x) = x ^ 2를 설정하겠습니다.

일반적으로, 함수 f의 그래프를 갖고 있다면 이를 y축과 x축을 교환하는 것으로 함수 f의 역함수의 그래프 역시 그려낼 수 있습니다. 다르게 말해서, 함수 f의 역함수의 그래프는 y = x를 기준으로 함수 f의 그래프를 반전시킨 것이라고도 할 수 있습니다. 이는 dy/dx가 함수 f에 대한 접선의 기울기라면 dx/dy가 함수 f의 역함수의 기울기가 될 것이라는 말입니다. 이 사실을 증명하기 위해 도함수의 정의를 이용할 수도 있지만, 음함수의 미분법을 사용하는 것이 더 쉽습니다.
$$\begin{align*}
y &= f(x)\\
f^{-1}(y) &= x\\
\frac{d}{dx}(f^{-1}(y)) &= \frac{d}{dx}(x) = 1
\end{align*}$$
연쇄 법칙에 의해 다음과 같이 됩니다.
$$\begin{align*}
\frac{d}{dy}(f^{-1}(y))\frac{dy}{dx} &= 1\\
\therefore \frac{d}{dy}(f^{-1}(y)) &= \frac{1}{\frac{dy}{dx}}
\end{align*}$$
이렇게 음함수의 미분법을 통해 원래 함수인 함수 f의 도함수를 알고 있다면, 이 함수의 역함수의 도함수 역시 알아낼 수 있다는 사실을 알게 되었습니다.
Derivative of arctan(x)
이제 역함수의 미분법을 알게 되었으니, 이를 이용해서 탄젠트 함수의 역함수인 아크탄젠트 함수의 도함수를 구해보겠습니다. 우선, 양변에 탄젠트 함수를 취하여 다음과 같이 정리하도록 하겠습니다.
$$\begin{align*}
y &= \textrm{tan}^{-1}x\\
\textrm{tan }y &= \textrm{tan}(\textrm{tan}^{-1}x)\\
\textrm{tan }y &= x
\end{align*}$$
어떻게 그려지게 될지 예측해 보기 위해 탄젠트 함수의 그래프를 그려보겠습니다.
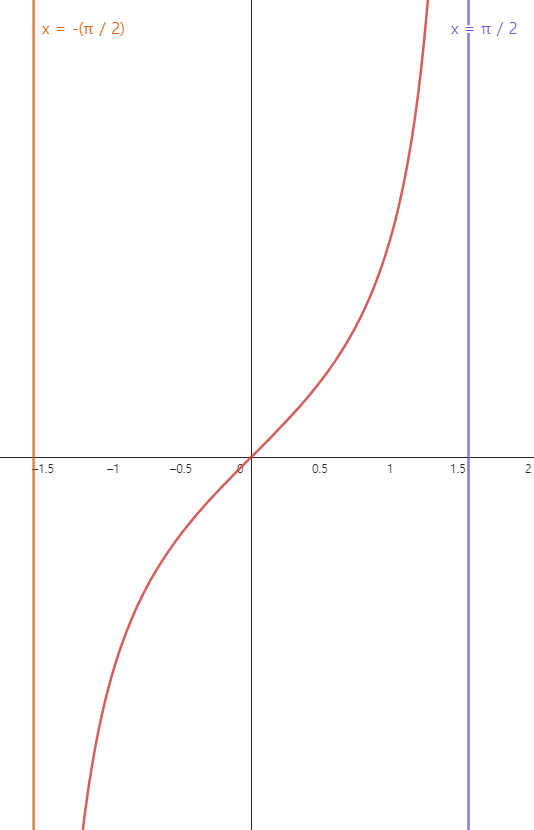
-π/2 < x < π/2에서 정의되어 있고, 음의 무한대에서 양의 무한대까지 뻗어나가는군요. 이 탄젠트 함수의 그래프를 y = x의 그래프를 기준으로 반전한다면 아크탄젠트 함수의 그래프를 얻을 수 있을 것입니다. 그렇게 되면 x의 범위와 y의 범위 역시 바뀌겠죠.
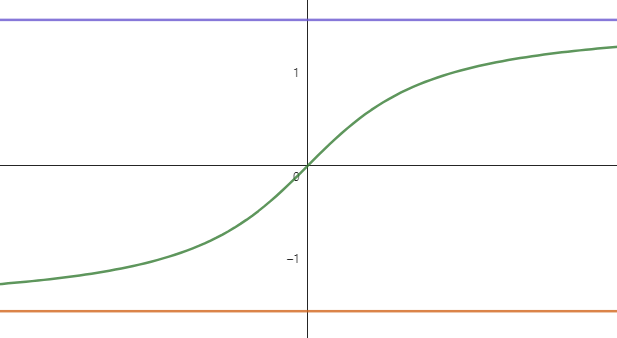
$$\begin{align*}
\frac{d}{dy}\textrm{tan }y &= \frac{d}{dy}\frac{\textrm{sin }y}{\textrm{cos }y}\\
&\vdots \\
&= \frac{1}{\textrm{cos}^2y}\\
&= \textrm{sec}^2y
\end{align*}$$
몫의 미분을 통해 위와 같은 사실은 이미 알고 있습니다. 이제 양변의 도함수를 구하기 위해 음함수의 미분법을 사용하겠습니다.
$$\begin{align*}
\textrm{tan }y &= x\\
\frac{d}{dx}(\textrm{tan}(y)) &= \frac{d}{dx}x\\
\frac{d}{dx}(\textrm{tan}(y)) &= 1\\
(\frac{1}{\textrm{cos}^2(y)})\frac{dy}{dx} &= 1\\
\frac{dy}{dx} &= \textrm{cos}^2(y)
\end{align*}$$
아쉽게도 우리는 x에 대한 도함수를 얻길 원하는 것이지, y에 대한 도함수를 얻고자 하는 것이 아닙니다. 따라서, 원래 공식인 y=arctan(x)를 대입해서 y'=cos^2(arctan(x))를 얻습니다. 이대로 끝내도 괜찮지만, 더 간소화할 수 있습니다.
tan(y) = x일 때, y=arctan(x)입니다. 피타고라스의 정리에 따라 빗변의 길이 h에 대해 다음이 성립합니다.
$$h=\sqrt{1 + x^2}$$
그리고 이제 다음과 같이 계산할 수 있습니다.
$$\textrm{cos}(y)=\frac{1}{\sqrt{1 + x^2}}$$
이것으로부터 다음과 같이 정리할 수 있습니다.
$$\begin{align*}
\textrm{cos}^2(y)=(\frac{1}{\sqrt{1 + x^2}})^2 &= \frac{1}{1 + x^2}\\
\therefore \frac{dy}{dx} &= \frac{1}{1 + x^2}
\end{align*}$$
따라서, 다음과 같이 마칠 수 있습니다.
$$\frac{d}{dx}\textrm{arctan}(x)=\frac{1}{1 + x^2}$$
Derivative of arcsin(x)
마지막 예시로, 아크사인의 도함수를 구해보겠습니다. 아크코사인의 경우에는 아크사인을 활용하면 쉽게 구할 수 있으니, 아크사인만 구하겠습니다. y=arcsin(x)인 식을 sin(y)=x로 고치겠습니다. 그 뒤에, 양 변의 도함수를 구해봅시다.
$$\begin{align*}
\textrm{sin }y &= x\\
(\textrm{cos }y)\cdot y' &= 1\\
y' &= \frac{1}{\textrm{cos }y}
\end{align*}$$
여기서, cos^2 x + sin^2 x = 1이라는 식을 이용하여 다음의 결과를 만들어냅시다.
$$\begin{align*}
\textrm{cos}^2y+\textrm{sin}^2y &= 1\\
\textrm{cos}^2y &= 1-\textrm{sin}^2y\\
\textrm{cos }y&= \sqrt{1 - \textrm{sin}^2y}
\end{align*}$$
이제 이 둘을 조합하여 다음의 결과로 이끌어냅시다.
$$y'=\frac{1}{\textrm{cos }y}=\frac{1}{\sqrt{1-\textrm{sin}^2y}}=\frac{1}{\sqrt{1-x^2}}$$
이렇게 아크사인의 도함수를 구했습니다.
다음 글에서 뵙겠습니다.
'Math > Single Variable Calculus' 카테고리의 다른 글
| Differentiation - Implicit Differentiation and Inverse Functions(3) (0) | 2023.04.28 |
|---|---|
| Differentiation - Implicit Differentiation and Inverse Functions(2) (0) | 2023.04.27 |
| Differentiation - Definition and Basic Rules(4) (0) | 2023.04.21 |
| Differentiation - Definition and Basic Rules(3) (0) | 2023.04.20 |
| Differentiation - Definition and Basic Rules(2) (0) | 2023.04.19 |


