Differentiation - Definition and Basic Rules(2)

지난 글에서, 기하학적으로 해석했을 때 도함수를 접선의 기울기로 정의했습니다. 1/x의 도함수를 구하는 과정을 예제로 풀어보았고, Power Rule을 증명해보기도 했습니다. 이번 글에서는 도함수를 변화율로 해석하고, 극한의 개념을 명확히 하며, 연속성을 설명하기 위해 극한을 사용하는 방법에 대해 설명하겠습니다.

---

Derivative as Rate of Change

---

전 글에 이어서 계속해서 도함수에 대해 이야기해보겠습니다. 앞서 서술한 것처럼 지난 글에서는 도함수를 기하학적 해석을 통해 접선의 기울기로 정의했습니다. 이번에는 도함수를 변화율로 해석하겠습니다.

Δx 만큼의 시간 동안 Δy 만큼 움직이는 물체의 위치를 기록한 함수 f가 있다고 하겠습니다. Δy/Δx는 해당 시간동안 움직인 물체의 위치의 평균 변화율이라고 할 수 있습니다. 다르게 말하자면, 물체가 움직인 평균 속도라고 할 수 있겠습니다. 이를 극한을 통해 한 순간으로 보일 만큼 구간의 간격을 줄이게 되면 이를 순간 변화율이라고 하고, 해당 순간에서의 속도라고도 할 수 있습니다. 예시를 더 들어보겠습니다.

---

Physical Interpretation of Derivative

---

앞선 설명을 통해 도함수가 변화율을 의미한다고 생각할 수 있습니다. 도함수에 대해 이러한 생각으로 접근을 한다면 물리 문제를 해결하는데 매우 유용하게 사용할 수 있습니다. 간단한 예시를 들어보자면, q를 전하의 양이라 하고 t를 시간이라 할 때, 다음은 전류(전하의 변화)를 의미합니다.

$$\frac{dq}{dt}$$

이런 식으로 응용이 가능하죠. 앞서 보여준 속도의 예시를 조금 더 구체적으로 설명해 볼까요?

100m 높이의 건물에서 물체를 떨어뜨릴 때,  지상에서의 높이 h는 다음과 같이 구할 수 있다고 가정하겠습니다.

$$h=100 - 4t^2$$

물체를 떨어뜨린 직후(t=0)일 때의 높이는 100m(h=100)입니다. 그리고 5초가 지난 뒤(t=5)에는 지면에 도착하겠죠(h=100 - 4 * 5^2 = 0). 이를 이용해서 물체의 평균 속도를 구해보자면 다음과 같습니다.

$$\frac{\Delta h}{\Delta t}=\frac{\textrm{distance traveld}}{\textrm{time elapsed}}=\frac{0-100\textrm{ meters}}{5-0\textrm{ seconds}}=-20\textrm{ m/s}$$

*분자의 0 - 80은 80 - 0을 오기한 것이 아닙니다.  

위와 같은 계산을 통해 평균 속도는 20 m/s라고 대답할 수 있습니다. 그런데 보통 평균 속도에 대해 신경을 쓰진 않죠. 호박이 땅에 떨어지는 순간의 속도를 더 궁금해할 것입니다. 이 순간 속도를 구하기 위해 h의 도함수 h'을 구하고, 5초일 때(t=5)의 순간 속도를 알아보겠습니다.

$$\frac{d}{dt}h=0-8t=-8t$$

이전 글을 잘 보았다면, 이 과정에 대해 더 설명할 필요는 없을 것 같습니다. 그럼 5초일 때의 순간 속도를 알아볼까요?

$$h'(5)=-8 * 5 = -40\textrm{ m/s}$$

시속 144 km/h에 해당하는 어마어마한 속도였습니다. 수가 음수로 나오는 이유는 건물의 높이를 측정할 때에는 지면으로부터 재기 때문이고, 물체의 이동 방향은 측정 방향의 반대 방향인 지면으로 향해있기 때문입니다.

이처럼 시간이 지남에 따른 변화를 연구하는데 활용이 가능하고, 그 외의 문제에도 활용이 가능합니다. 이상으로 도함수에 대한 소개를 대략적으로 마치겠습니다. 이젠 익숙해지셨으리라 믿습니다.

---

Limits

---

지난 글에서 할선이 극한을 통해 접선에 가까워지는 과정에 대해 다뤘고, Δx가 0에 접근함에 따라 Δy/Δx가  y'=dy/dx인 극한으로 가는 것에 대해 설명했습니다. 이제 극한과 연속성에 대해 조금 더 체계적으로 다뤄보겠습니다. 앞으로 다룰 많은 공식들을 도출하기 위한 개념입니다. 우선 간단한 함수의 극한을 통해 쉬운 단계부터 시작하도록 하겠습니다.

$$\displaystyle \lim_{\Delta x \to 3}f(x)=\displaystyle \lim_{\Delta x \to 3}\frac{x^2 + x}{x + 1}=\frac{3^2 + 3}{3 + 1}=\frac{12}{4}=3$$

매우 간단한 극한입니다. 단순히 극한값을 대입하는 것만으로도 정답을 얻어낼 수 있습니다. 왜냐하면 x가 3에 가까워짐에 따라 f(x)는 f(3)에 가까워지기 때문입니다. 하지만 항상 이렇게 쉬울 수는 없는 법입니다.

$$\displaystyle \lim_{\Delta x \to 0}\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$$

이전 게시글에서 도함수를 구할 때 사용했던 공식입니다. Δx에 0을 바로 대입하면 0/0 꼴이 되어버립니다. 분모가 0이 되어버리는 것이죠. 이를 피하기 위해 Δx를 소거할 필요가 있습니다.

$$\displaystyle \lim_{\Delta x \to -1}\frac{x^2 + x}{x + 1}$$

$$\displaystyle \lim_{\Delta x \to \infty}\frac{x^2 + x}{x + 1}$$

위와 같은 경우처럼 분모가 0이 되어버림에 따라 곧바로 계산을 할 수 없을지도 모르고, 어쩌면 극한값이 없을 수도 있습니다.

극한에 대해 조금 더 쉽게 설명할 수 있도록, 개념을 몇 개 더 소개할까 합니다. 바로 좌극한과 우극한입니다.

$$\displaystyle \lim_{x \to a^+}f(x)$$

이러한 표기법이 우극한으로, 극한을 계산할 때 x를 a에 가까워지지만 a보다는 큰 값으로 사용할 것을 의미합니다.

$$f(x)\begin{cases}
x + 1 &\text{ if } x>0\\
-x & \text{ if } x\leq0 
\end{cases}$$

위와 같은 함수가 있다고 할 때, x를 0의 우극한으로 계산하자면, f가 x + 1이 됨에 따라 1이라는 극한값을 얻을 수 있게 됩니다. 극한을 계산할 때 x를 a에 가까워지지만 a보다는 작은 값으로 사용할 생각이라면 좌극한을 사용할 수 있습니다.

$$\displaystyle \lim_{x \to a^-}f(x)=0$$

이렇게 되면 극한값은 0을 얻을 수 있을 것입니다.

Figure 1: Graph of f(x)

좌극한과 우극한에 대한 개념은 연속성에 대해 설명할 때 좀 더 쉽게 이해할 수 있도록 도움이 될 것입니다. 

---

Continuity

---

이제 연속성이 대해 설명하겠습니다. f가 a에서 연속적이라는 것은 x가 a로 가는 극한값을 취했을 때 함수 f의 극한값이 f(a)와 같음을 의미합니다. 설명을 더 해보자면, a에서 연속인 함수는 다음과 같은 속성을 가집니다.

• 함수 f가 a에서의 좌극한값과 우극한값이 존재함
• 함수 f가 a에서의 값인 f(a)가 정의되어 있음
• 함수 f가 a에서의 좌극한값과 우극한값이 같고, 이 값이 a에서의 값인 f(a)와 같음

너무 당연한 소리처럼 보이겠지만, 극한을 계산할 때 절대로 x가 a와 같다고 하면 안 됩니다. f(a)와 x가 a로 가는 극한값을 가질 때의 f의 값은 서로 독자적으로 계산되어야 합니다. 위에서 보았던 그저 x에 a를 대입만 하면 되었던 쉬운 예시는 함수 f가 연속했기 때문이었습니다. 이젠 극한을 구하기 힘든 불연속 함수들에 대해 살펴보겠습니다.

---

Discontinuity

---

불연속의 종류는 다양합니다. 위에서 설명한 연속의 조건들을 하나씩 없애보면서 발견이 가능한데, 우선 살펴볼 것은 좌극한값과 우극한값이 존재하지만, 이 둘이 서로 같지 않을 때입니다. 이를 점프 불연속성(Jump Discontinuity)이라고 하는데, 위에서 이미 예시를 보았습니다.

$$f(x)\begin{cases}  x + 1 &\text{ if } x>0\\  -x & \text{ if } x\leq0  \end{cases}$$

x가 0보다 클 때에는 0에서의 극한값이 1이지만, f(0)은 0입니다.

Figure 2: Another example of a jump discontinuity

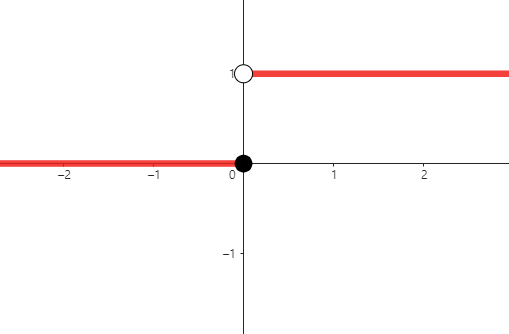
물론 이런 형태로 Figure 1의 형태 외의 점프 불연속성이 발견될 수 있습니다. 그런데, x가 a로 갈 때의 좌극한과 우극한이 같지만 f(a)가 해당 값들과 다른 경우도 있습니다. 이를 제거 가능한 불연속성(Removable Discontinuitiy)라고 합니다. 다음과 같은 경우죠.

$$\displaystyle \lim_{x \to a^+}f(x)=\displaystyle \lim_{x \to a^-}f(x)\neq f(a)$$

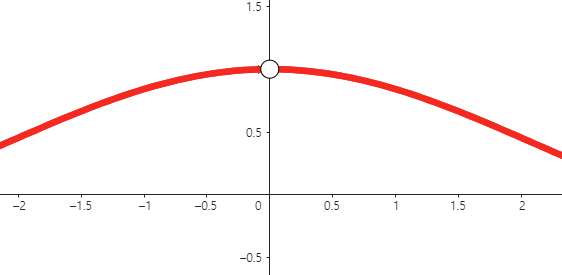
이처럼 좌극한과 우극한의 값이 같지만, 해당 지점에서의 값이 정의되지 않거나 극한값과 다름으로 인해 불연속이 되는 경우입니다. 이러한 극한은 함수를 재정의하는 것으로 해결이 가능한데, 이것이 왜 이 불연속성을 제거 가능한 불연속성이라고 부르는지에 대한 이유입니다.

$$g(x)=\frac{sin(x)}{x}$$

대표적인 예시로는 위와 같은 함수가 있습니다. 극한으로 갔을 때 x가 0이 되어 정의되지 않는데, 나중에 다룰 내용이지만 이 함수는 0에서의 극한값으로 1을 갖습니다. 분모가 0 임에도 불구하고 x=0일 때 제거 가능한 불연속성을 갖는 것이죠.

Figure 3: A removable discontinuity: the function is continuous everywhere except one point

그렇다면 우극한과 좌극한 모두 무한으로 가면 어떻게 될까요? 둘 다 양의 무한대일 수도 있고, 음의 무한대일 수도 있고, 서로 다른 부호를 가질 수도 있습니다. 이러한 불연속을 무한 불연속성(Infinite Discontinuity)라고 합니다.

Figure 4: An example of an infinite discontinuity: 1/x

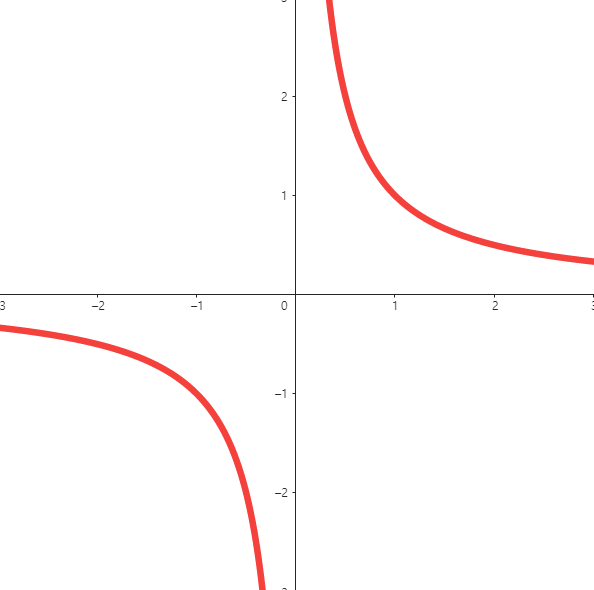
Figure 4를 보면, 0으로의 우극한값은 양의 무한대인 반면, 좌극한값은 음의 무한대입니다. 양의 무한대와 음의 무한대는 다른 것이기 때문에 0에서의 극한값으로 무한대라고 할 수도 없는 처지입니다.

Figure 5: An example of an ugly discontinuity: a function that oscillnates a lot as it approaches the origin

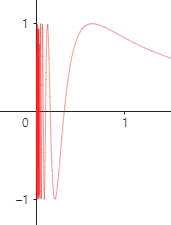
이런 불연속성도 있습니다. 위의 그림은 y=sin(1/x)의 그래프인데, sin(1/x)는 x가 0으로 갈 때 정의되지 않습니다. x가 0으로 갈 때 좌극한값도 존재하지 않고, 우극한값도 존재하지 않습니다. 그저 진동할 뿐이죠...

---

Differentiable Implies Continuous

---

미분가능성에 대해 알아보겠습니다. 미분가능하면 연속입니다. 다르게 말해서, a에서 도함수 f'의 값이 존재하면 f는 a에서 연속입니다.

$$\displaystyle \lim_{x \to a}f(x)-f(a)=0$$

위 사실을 보여주면 되겠죠.

$$\displaystyle \lim_{x \to a}f(x)-f(a)\begin{align*}\\
&= \displaystyle \lim_{x \to a}\frac{f(x)-f(a)}{x-a}(x-a)\\
&= f'(x)\cdot 0\\
&= 0
\end{align*}$$

함수 f가 미분가능하다는 가정을 하고 도출한 결과입니다. x-a를 곱하고 나눌 때 0으로 곱하고 나눈다는 착각을 할 수도 있지만, 극한의 성질 때문에 x가 a와 무한히 가까워질 뿐, a와 같지는 않기 때문에 가능한 연산입니다. 아무튼, 이렇게 미분 가능하면 연속이라는 사실을 알려드립니다.

다음 글에서 뵙겠습니다.